METEOROLOGIE en 1916 ( 2ème partie)

METEOROLOGIE en 1916 

Article  écrit par Alain F6AGV -  BHAF

A- Pourquoi la météorologie ?

C'est l'étude des différents phénomènes physiques qui se manifestent sur la Terre et dans l' atmosphère.
On étudie les variations de température, de la pression atmosphérique, et de l'humidité.
Cela va aussi par la connaissance des vents, des précipitations, en général des mouvements de l'air dans tous les sens et les courants marins.
Pour compléter les éléments physiques, nous ajouterons :
la pesanteur, le magnétisme de la Terre, l'électricité atmosphérique, les phénomènes lumineux comme l'arc en ciel, les halos, le Soleil, la Lune et ses marées...
On distinguera deux grandes parties :
--- la climatologie 
--- la météorologie dynamique
La climatologie est l'étude dont les phénomènes météorologiques se produisent pour chaque lieu de la Terre.
Influence des topographies, et des conditions géographiques.
Il faut tenir compte aussi de la nature, avec le développement et la répartition des végétaux, la présence des animaux, la présence des habitations, des villes.
La météorologie dynamique tient compte des lois générales des mouvements de l' atmosphère, le mode de formation des tempêtes, des tornades, des formations orageuses...
Ces deux parties sont dépendantes l'une de l'autre.

Les variations : 
Il faut admettre quand on étudie l'atmosphère que toutes les valeurs des éléments sont soumises à des variations incessantes. Ainsi une radiosonde qui vient de faire des mesures à un instant et une position donnée, transmet des valeurs qui sont seulement valables à l'instant t.
Pendant le vol, les paramètres mesurés ne correspondent plus aux valeurs des éléments aux différents points qui ont été traversés. Mais les périodes sont courtes et il faut évaluer dans quel sens se font les variations.
Il y a des variations périodiques ou régulières, par exemple la température de l'air en fonction de la hauteur du Soleil dans le courant de la journée.
Les hauteurs des marées sont périodiques et peuvent se prévoir suivant la position de la Lune.
Il y a des variations irrégulières ou perturbations, qui viennent modifier la régularité des variations périodiques et même les modifier complétement.

La méthode des moyennes :
La connaissance des variations devient parfois très complexe. Il est fait appel à une méthode des moyennes, qui permet de simplifier le problème mais qui doit être utilisée avec discernement.
Par exemple, nous pouvons mesurer les valeurs successives d'un paramètre météorologique, pendant une certaine période, et calculer la valeur moyenne.
On notera l'écart supérieur et l'écart inférieur, sur un paramètre comme la température d'un lieu ou la pression.

 

Les surfaces  amm’n   et   aa’n’n sont égales  et  am  est la hauteur moyenne. 

Les surfaces  ma’p   et   pm’n’  sont égales.   p étant le point d’intersection avec la droite mm’.

Ce qui implique que mm’ est bien la moyenne.   

On peut appliquer ce graphe en météorologie pour par exemple la quantité de chaleur.

Elle est variable de a’  à   n’.

Elle est constante de m  à  m’.  Mais la quantité de chaleur totale est la même dans les deux cas.

Pour les calculs on assimilera les valeurs physiques  aux longueurs :    aa’   pour  a0,  bb’  pour  a1  et ainsi de suite…

Formules de quadrature : 

On divise la base du graphe  a n   en  n  parties d’égales longueurs.   Voir  le dessin en haut à droite.

formule des trapèzes :    on assimilera l’arc d’une courbe à la corde, l’erreur est inférieure aux erreurs de mesures.

Voir le croquis ci-dessus.

Surface d’un trapèze :   AA’B’B 

S   =    (AB *  BB’)  +  1/2* ( AB  *  (AA’-BB’))   =   AB *  BB’   +    1/2(AB*AA’)   -   1/2(AB * BB’)

S  =     AB/2  *   (   AA’   +   BB’  )   =    Hmoy  *   AB     

Hmoy   =     S   /    AB    =    1/2  *    (   AA’   +    BB’  )    

On remplace  AA’   par   a0     et    BB’   par   a1      :      Hmoy   =     1/2   *    (   a0   +   a1  )   =   1   *   (  a0/2  +  a1/2  )

AN   :    AB   =    7      AA’  =  a0   =   7      BB’  =   a1   =   5       réponse  Hmoy   =   6  

formule générale :       Hmoy  =   1 /n    (   a0/2   +   a1   +  a2  + ….        +  an/ 2   )  

Retour sur l’application numérique :     avec   a0 =  7    a1  =  5    et    n  =   1        avec       an  =   a1   

Hmoy   =     1/1    (    7/2    +   0    +   0   …..   +   5 /2    )    =     3,5   +   2,5   =    6   

Autre exemple :

 

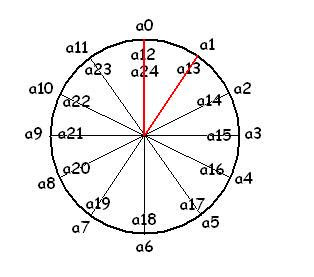
Température moyenne sur une journée de 24 heures :   de  minuit à  minuit  

Première valeur  à  minuit   :    a0   

Valeur  à   1 heure du matin    :     a1

Il y a 23 valeurs de  1  heure du matin  jusque  23 heures du soir   :    de  a1    à   a23  

Dernière valeur  à  minuit   :    a24  

n =  24    car   il y a 24  intervalles !    Voir le croquis  ci-dessus.

Application de la formule :     Tmoy  =   1 /24   *   ( a0/2   +   a1   +  a2  +  …….  +  a23  +   a24/2  )   

                                                                                                                                                                      

Autre  exemple   :    

                                                                        

Première valeur  à  minuit :    a0  

Seconde valeur  à  1  heure   :    a1

n =  1   

Application de la formule :       Tmoy  =   1/1    *    (  a0/2   +  ..............      +   a1/2    )  

Moyenne arithmétique :  

Il est  facile d’additionner toutes les valeurs prises toutes les heures (ou à intervalle régulier), ou toutes les trois heures.

Et de diviser le total par le nombre de valeurs pour trouver la valeur moyenne.

exemple :      Il y a 5 températures       Tmoy  =   (   25 +  23  +  22 +  24  +  26   )  /   5     =    24   °C  

avec  la formule précédente     Tmoy   =   1/ 4  *   (   25/2   +   23   +  22  +   24   +  26/2   )    =    23,7  °C   

L’erreur entre les deux méthodes n’est pas significative.  

Autre exemple :    prendre les valeurs toutes les 3 heures sur READY 

0Z,    3Z,    6Z,    9Z,    12Z,    15Z,    18Z,    21Z,   0Z,  

a0      a1     a2      a3      a4       a5       a6       a7       a8  

n = 8   car   8 intervalles  

Tmoy1 =   1/8   *    (  a0/2    +  a1  + a2  + a3  +  a4  +  a5  + a6  +  a7  +  a8/2  )

Tmoy2 =    (  a0  +  a1  + a2  +  a3 +  a4 +  a5  +  a6  +  a7  +  a8  )  /  9

AN   :   

a0      a1     a2     a3     a4     a5     a6     a7     a8  

4        3       2      1       3       4      6       5       4

Réponses    :     Tmoy1  =   3,5  °C       et     Tmoy2  =   3,6  °C 

Moyenne de la journée   :

Jour  1    =   a0  

Jour  2    =   a1

Jour  3    =   a3  …….   

Moyenne pour un mois    :        Mmoy  =   Somme de 1  à  31   /    31         pour  31 jours / mois

Moyenne pour une année :        Mmoy =   Somme de  1  à  365  /  365       pour  365  jours / mois 

Faire une somme de 365 jours prend du temps, on peut faire la moyenne annuelle des moyennes mensuelles.

                                                Mmoy   =   Somme de 1 à  12  /  12

JAN    FEV    MAR    AVR    MAI    JUN    JUL    AOU    SEP    OCT    NOV    DEC

A1       A2      A3        A4        A5      A6       A7      A8       A9      A10     A11      A12

Mannée   =    1/12   *   (   A1  +   A2 + ………..A12  )

Mannée   =    1/365  *  (   31*A1  +   28*A2  +  31*A3 …………  +  31* A12  )

A1  est   la moyenne journalière  du  mois de Janvier 

Pour les années bissextiles :    Mannée   =   1/366 *  (  31*A1  +  29*A2 + …..     +  31*A12 )

Dans la pratique on prendra comme moyenne annuelle, la moyenne arithmétique des 12 moyennes mensuelles. 

A    suivre,

Alain F6AGV  -     BHAF   10/ 2015