Variation
de la vitesse de montée d’un ballon
Un ballon stratosphérique
est constitué d’une enveloppe latex contenant une quantité
d’hélium (gaz plus léger que l’air) et une nacelle ou boitier
électronique, dont le rôle de charge utile est d’embarquer des
capteurs ainsi qu’un émetteur radio qui va
transmettre les données
directement vers le sol à l’intention des stations d’écoute.
On a pris l’habitude de
considérer la vitesse de montée constante pendant un vol. Mais les
relevés montrent qu’il n’en est rien.
Une approximation utile
est donnée par la connaissance de l’altitude d’éclatement en
fin de montée, et le temps mis pour y arriver.
Exemple :
éclatement pour 32000 mètres et temps de montée 2 heures.
Ce qui fait une moyenne de
32000/7200 = 4,44 m/s.
Relevés d’une
radiosonde : exemple
En bleu, la vitesse
calculée suivant la résistance de l’air R et en rose, les relevés
de vitesse de montée transmis par la radiosonde.
Vitesse calculée :
elle est issue des données fournies par la radiosonde, la pression,
la température et les paramètres du ballon Ceci est traité dans
un ordre logique.
Exemple :
Vitesse donnée par la
M10 en fonction de l’altitude :
Vitesse de montée du
décollage à l’éclatement : (ne
jamais dire « explosion »)
Remarque :
la vitesse va en augmentant au fur et à mesure de la montée. On le
constate sur la courbe de l’altitude en fonction du temps,
ci-dessous après l’altitude de 15000 m jusqu’à l’éclatement
au point culminant du vol.
Pour cette courbe de
l’altitude en fonction du temps, la vitesse de montée est de 5m/s
avant 15000 m et elle devient 5,5 m/s entre 15000 m et
26000 m. Pour la durée de la montée, on arrive à 26000 m en 5000
s, d’où Vmoy = 5,2 m/s
Facteurs qui influent
sur la vitesse de montée :
La vitesse de montée
instantanée va connaître des variations comme on peut le constater
en regardant les graphes ci-dessus.
Pendant la traversée de
l’atmosphère, suivant les couches, la masse volumique de l’air
peut varier, cela signifie que la température de l’air varie ainsi
que la pression. Il peut y avoir des courants ascendants ou
descendants. Il y a des nuages jusque 10000 ou 12000 m.
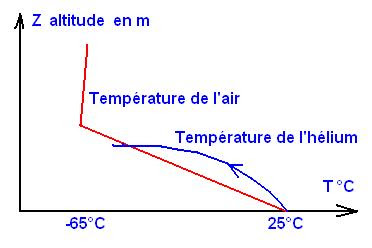
La température de
l’hélium peut être différente de celle de l’air. En effet,
l’hélium va se refroidir, l’air aussi, on considère un échange thermique entre
l’enveloppe et l’atmosphère, dans les deux sens !
Le rayonnement solaire
intervient dans les échanges thermiques, l’enveloppe reçoit et
rayonne une énergie calorifique.
Il est donc très
difficile de tenir compte de tous les paramètres physiques présents
pendant un vol de ballon.
Il faut procéder à des
mesures : capteurs…
Par contre, il est
important de récupérer les données et de les interpréter ensuite!
Considérations sur les
calculs :
Il n’est pas inutile de
chercher quelques explications pour en savoir un peu plus sur le vol
réel d’un ballon. Cette motivation est renforcée par le fait
qu’il est intéressant de comprendre et de se lancer dans des
calculs, aussi bien pour un amateur que pour un étudiant ou un
enseignant ou chercheur en météo. Les amateurs sont très actifs
dans les domaines de l’espace, de l’astronomie et de la
météorologie. Le mot « amateur » est parfois peu
judicieux et sujet à confusion.
Etude dynamique :
Système simplifié : l’enveloppe
Latex fermée
On ne considère que les
forces qui s’exercent sur le ballon (l’enveloppe latex) au
centre d’inertie (O).
Pa : la poussée d’
Archimède en N ( poids du volume d’air situé au même niveau
)
P : le poids total avec
l’hélium en N
R : la traînée ou
résistance de l’air s’opposant contre le mouvement du ballon
vers le haut.
On négligera les forces
sur les autres éléments de la chaine de vol, comme la nacelle et le
parachute dans un premier temps.
On étudie le bilan des
forces sur un axe vertical Oy dirigé vers le haut, et les forces
sont appliquées au centre de gravité (O).
A t= 0s
la vitesse de montée (v) est nulle ainsi que l’accélération qui
est la dérivée de la vitesse (dv/dt).
Recherche de l’équation
de base : le signe indiquant le sens. + vers le haut et
- vers le bas.
P = - m
. g Pa = rhoair . V . g R = - 1/2 .
Cx . rhoair . S . v^2 Phe =
- rhoHe . V . g
L’équation de base est
alors :
Fal = V . g . (
rhoair - rhoHe ) - m(sauf He) . g = 1/2. Cx
. rhoair . S . v^2 = m dv / dt
Explication importante :
la masse d’hélium injectée dans un ballon fermé est constante :
(sans fuite)
rhoHe = mHe / V ou
mHe = rhoHe . V
le poids de l’hélium
est V . g . rhoHe = mHe . g
P le poids total avec
l’hélium est égal au poids de l’enveloppe + le poids de
l’hélium P = - m . g
L’équation de base
devient : Fal = rhoair.V.g - m . g = 1/2 . Cx .
rhoair . S . v^2 = m . dv / dt
On peut en
déduire « l’équation différentielle »
suivante : Pa - P - R = m . dv / dt ( Loi de
Newton)
m .
dv/dt = rhoair . V . g - m . g - 1/2 . Cx . rhoair . S . v^2
dv / dt
= - ( Cx . rhoair . S . v^2 ) / 2 m + 1 / m .
( rhoair . V . g - m . g )
dv / dt
= - ( Cx . rhoair . S . v^2 ) / 2 . m + g ((
rhoair . V / m ) - 1 )
de la forme : dv / dt
= - A . v^2 + B ( résolution par la méthode d’EULER).
Voir document, on ne
traitera pas cette question ici.
il y a une accélération
au décollage pendant quelques secondes et la vitesse se stabilise à
une valeur limite Vlim :
dv / dt = 0 = -A
. v^2 + B
v^2 = B / A
Vlim = racine de B / A
La courbe de l’altitude
en fonction du temps prouve que la vitesse n’est pas limitée, mais
qu’elle augmente un peu.
Mais les méthodes de
calculs ne sont pas les mêmes mais non contradictoires.
Application numérique
avec des valeurs réelles :
Volume d’hélium injecté
dans l’enveloppe : 5 m^3 Voir méthode avec le
manomètre.
altitude initiale du
sol : Z = 220 m
pression mesurée au sol :
P = 987 hPa
température au sol :
T°C = 26,9 °C
Humidité relative :
Hu = 45%
masse du parachute :
0,1 kg
masse de la nacelle :
0,975 kg (avec piles)
masse de l’enveloppe :
1,6 kg
masse du réflecteur radar
passif : 0,06 kg
masse de la ficelle :
0,05 kg
masse du tracker M10 :
1,50 kg (avec piles)
Cx de l’enveloppe
gonflée : 0,5515
Bidon tare vide :
0,6 kg
Tuyau raccord entre
détendeur et manchon : 0,3 kg
On demande de
préciser :
A--- la masse d’hélium
injectée : mHe en kg
sachant que mHe =
P . V / R . T P en pascal, V en m^3, R = 2063, T
en kelvin (T°C + 273,15)
B--- la masse volumique de
l’air : rhoair en kg/m^3
sachant que rhoair =
P / R . T P en pascal R = 287,5 T en
kelvin
C--- la masse sauf
hélium : en kg
D--- le diamètre de
l’enveloppe au décollage en m
E--- la section S de
l’enveloppe en m^2
F--- déterminez les
facteurs A = ( Rhoair . Cx . s ) / 2 . m et B =
g . (( rhoair . V / m ) - 1 )
G--- déterminez la
vitesse limite au décollage.
H--- déterminez la Fal
en kg.
I--- on décide de mesurer
la Fal avec le dispositif ci-dessus.
1- bouteille d’hélium
2- détendeur de pression
avec manomètre 250 bars
3- tuyau entre détendeur
et manchon enveloppe
4- raccord avec le manchon
5- enveloppe latex
6- dynamomètre
7- bidon plastique de 5
litres ( provenant de liquide lave-glace )
Cette mesure ne peut se
faire que par vent nul ou sous un hangar fermé.
On fera les calculs avec
le dispositif simplifié : sans tenir compte de la résistance
de l’air.
Pa : poussée
d’Archimède en kg
Phe : poids (ou
masse) d’hélium injectée
P : poids de
l’enveloppe latex
T : poids de la
tare ( 7 + 3 )
Sachant que le système
présenté ci-dessus est en équilibre avec le ballon flottant,
on demande :
---- d’écrire la
relation littérale de la Fal en configuration de vol, selon la
figure en haut de la page, avec Fal = f(Pa, Phe et P)
---- d’écrire la
relation littérale à l’équilibre de la figure ci-dessus, avec
Pa, Phe, et T
Déduire la relation
donnant la valeur de T :
J--- Avec l’analyse de
la question I, et les valeurs numériques
la charge est rajoutée à
P, sous forme d’un poids équivalent à l’ensemble de la chaine
de vol réelle.
Déduire la valeur de la
quantité d’eau à placer dans le bidon plastique pour obtenir
l’équilibre.
Nota : cette méthode
de pesée est utilisée par les centres météo comme Trappes quand
il y a un opérateur chargé
du lâcher et non une
cabine automatique. La tare est alors un poids toujours le même pour
un type de radiosonde.
ANNEXE :
On a admis que le ballon
se déplace à la même vitesse que le vent. Mais pour des structures
de ballon de grande dimension, avec une hauteur importante, il peut y
avoir une différence entre la vitesse en haut et la vitesse en bas,
donc production de vibrations ou
de mouvements pendulaires
ainsi que des rotations de l’ensemble de la chaine de vol. La
ficelle de cette chaine étant élastique, elle restitue le mouvement
en sens inverse et la nacelle peut tourner par exemple à 10 tours
par minutes. L’enveloppe possède un peu plus d’inertie et va
tourner moins rapidement que la nacelle…
L’enveloppe latex va
augmenter son volume au fur et à mesure de la montée et cela
compense la perte de la masse volumique de l’air ambiant. La
poussée d’ Archimède étant égale à rhoair . V . g
On peut remarquer que
rhoair diminue et que V augmente.
La pression interne
s’équilibre avec la pression externe, mais l’enveloppe se dilate
et le latex finit par éclater en commençant par un point faible du
à la fabrication. Suivant la qualité, l’enveloppe tiendra
jusqu’au volume d’éclatement donné par le fabriquant.
Mais on a parfois des
surprises avec une enveloppe qui éclate prématurément ou va plus
haut que prévu ?
La physique du ballon
pendant son vol est très complexe, et dans des études
expérimentales, il serait possible de capter,
quelques paramètres
intéressants :
--- température interne à
l’enveloppe
--- pression interne
--- infrarouge soleil
--- infrarouge ballon
--- infrarouge de la
terre.
Comment évolue la
température de l’hélium pendant le vol ?
On sait que le volume
d’hélium est :
V = mHe . R . T /
P R 2063 T en kelvin et P en pascal
( P hPa x 100 )
A remarquer que la masse
d’hélium injectée reste constante pendant le vol, si l’enveloppe
n’est pas poreuse ou percée !
Par contre le poids va
varier suivant la valeur locale de g accélération de la pesanteur
en fonction de l’altitude.
Dans les calculs on
prendra le choix de travailler avec les masses, mais la traînée de
résistance de l’air est exprimée en newton.
Fal en kg x g =
R en newton
Les référentiels :
On peut distinguer le
référentiel terrestre supposé galiléen et un référentiel lié
au ballon.
Pour un passager du
ballon, il n’y aurait pas de vent et seulement une montée (ou une
descente).
Des expérimentations sont
basées là-dessus pour mesurer la masse volumique de l’air avec
une surface plane reliée à une balance !
Il est tout à fait
possible de faire des prévisions de trajectoire, et de la
cartographie à partir des informations précises sur les vents (force et direction). Ces
données précieuses restent valables pendant une période suffisante
pour faire des prévisions.
Si on cumule des
prévisions à intervalle réguliers, il faut alors s’intéresser
aux tendances des variations des forces et des directions.
Les meilleures prévisions
se font 6 heures avant un lâcher. A la rigueur 12h avant. Ou mieux
au fur et à mesure de l’arrivée des données météo
pendant un vol en temps réel.
On fait parfois des
prévisions à postériori, avec les données H-0, pour comparer les
prévisions et les valeurs effectives, et ajuster les paramètres du vol
(les vitesses de montée et de descente).
C’est pourquoi, il est
impératif de connaître avec précision les coordonnées du point
d’impact réel sur le terrain et l’état du parachute. Etat,
suivant son ouverture : bonne, moyenne ou mauvaise. Si
possible, notez la surface offerte au freinage
par rapport à une
ouverture à 100%. Le parachute fera l’objet d’un autre document.
Suspentes emmêlées : ouverture
à 70 %
Études proposées :
Dans l’ordre logique :
--- prévisions
--- décollage
--- montée et éclatement
--- descente sous
parachute
--- point d’impact
--- traitement des données
SOURCE : BHAF juillet 2017
- Alain Verbrugge F6AGV - BHAF -












Aucun commentaire:
Enregistrer un commentaire